前些年到三明市泰宁县的黄厝村，发现村民历代以玩土棋为乐。棋盘是镌刻在天然石头上，所以能够保留至今。据说原有二十多种，现存近十种（如图）。
其中的鸡母棋，小时侯在山上放牛玩过，福州地区称之为猪母猪仔棋。而豆腐棋引起特别兴趣，那不就是九宫图吗！
九个数字1，2，3，4，5，6，7，8，9按照一定规则一一分别置入九个方格，就是我国传统文化上的洛书！而洛书却是由神话传说“神龟负书”得来的。
图 1-1
请您将1，2，3，4，5，6，7，8，9一一填入方阵的九个方格，使得横3方格的数之和、竖3方格的数之和跟对角3方格的数之和相等，即横、竖、斜3方格的数之和都相等。
请问：
（1）横、竖、斜三数之和各是多少？
（2）您有几种不同的填数方法？ 构成的
（3）在您完成填数以后，发现横、竖、斜各数之间有什么关系？
解答：如果您填数正确，该数字方阵具有如下的特性：
（1）横、竖、斜3个数之和都是15，全部9个数之和为45。15是45的1/3。
3X3方阵构成了洛书（如右图），后来又称“纵横图”。方阵扩大到4X4方格，传到西方，由于其结构的奥妙、十分奇幻，被称作Magic Square，翻译为“幻方”。我们现在也采用“幻方”这称谓。
洛书是3阶幻方，横、竖、斜3数之和均为15，称作这个幻方的幻和。
（2）中央方格的数是5，其对称的两端两个方格的数字之和都相等：
9+1=10，3+7=10，6+4=10，2+8=10，
这样的幻方，称作中心对称幻方。10称作这个幻方的对称和。
（3）将图形旋转90°仍然保持横、竖、斜3数之和为15不变，还是幻方。翻转以后又得到4种，所以一个幻方经过旋转、翻转可以得到有8个不同的幻方。如图1-2，是左旋转得到的，如果采用右旋转，结果是一样的。您可以试试。
其它的特点和性质，以后还会遇到。
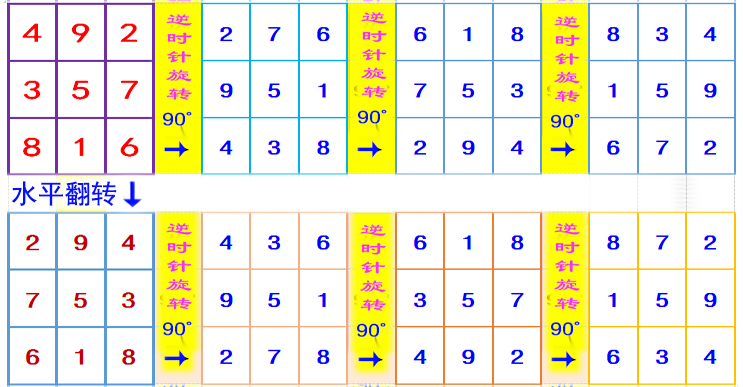
图1-2
（4）观察八个方阵可以发现：不论是旋转还是翻转，中央方格数字5是“巍然不动”的，以中央方格为中心的对策两端方格里数字之和都等于10。所以，对称幻方不论是旋转还是翻转，它的幻方特性是不变的。