三个6阶幻方，幻和111：6×（1+62）÷2=6×37÷2=111。
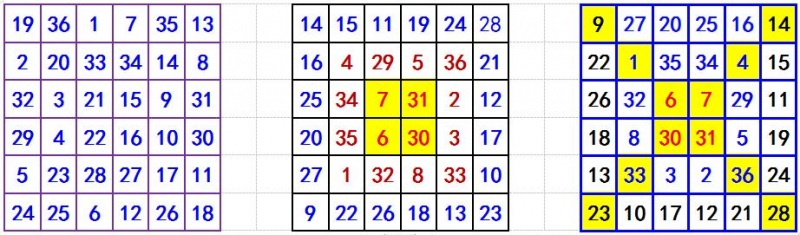
图5-1 图5-2 图5-3
图5-2对角线的方格里的数字是以方格中心点为对称的，两对称方格里的数字之和都是1+62=37，是对称幻方，对称和37；
图5-3对角线隔开的四区域，上下两梯形区域方格里的数字满足水平轴对称，而左右两梯形区域方格里的数字满足垂直轴对称。对称和都是1+62=37。
所以，图5-3是6阶双对称幻方，即6阶同心幻方。
这里关于6阶对称幻方、双对称幻方称谓的规定，对6阶以上的偶数阶幻方都是适用的。
|
4 |
29 |
5 |
36 |
|
34 |
7 |
31 |
2 |
|
35 |
6 |
30 |
3 |
|
1 |
32 |
8 |
33 |
图5-4
我们观察图5-2的内部4×4方阵(图5-4)，它的横、竖、斜（每行、每列和两条主对角线）10组方格里的数字之和都相等，都是74。这就引起关注：
对于大于等于3的整数n，构造n×n的方阵或表格，将1到n2的n2个数字填到方格中，使得每行、每列和两条主对角线上方格里的数字的和都相等，就构成了一个“幻方”。这种幻方称为“经典幻方”。
其实，n阶幻方中的数字，不一定是1到n2，将经典的n阶幻方的每一个数字都乘一个非0的正整数再加或减同一个整数，所得到的仍然满足每行、每列和两条主对角线上的数字和相等的条件，它被称为“广义幻方”，广义幻方还有很多不同的、花样繁多的种类。
因此，图5-4是一个广义幻方。
当然，如果没有特别说明，一般所说的幻方，就是指经典幻方。
而图5-2幻方是镶嵌了幻方5-4的幻方，我们就称图5-2还是“镶嵌幻方”。
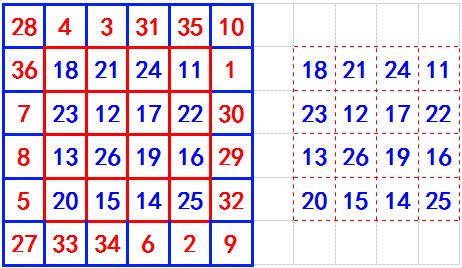图5-5是任勇校长为厦门第一中学设计的
6阶镶嵌幻方，作为校园数学广场铺设地面的景
观。
图5-6是内嵌的4阶广义幻方，幻和74。
请您观察图5-6里的方格，最小与最大的数是多少，。
存在什么奥妙的关系？ 图5-5 图
